ミッション
角すいや円すい、球の特ちょうを知り、体積を求められるようになりましょう。
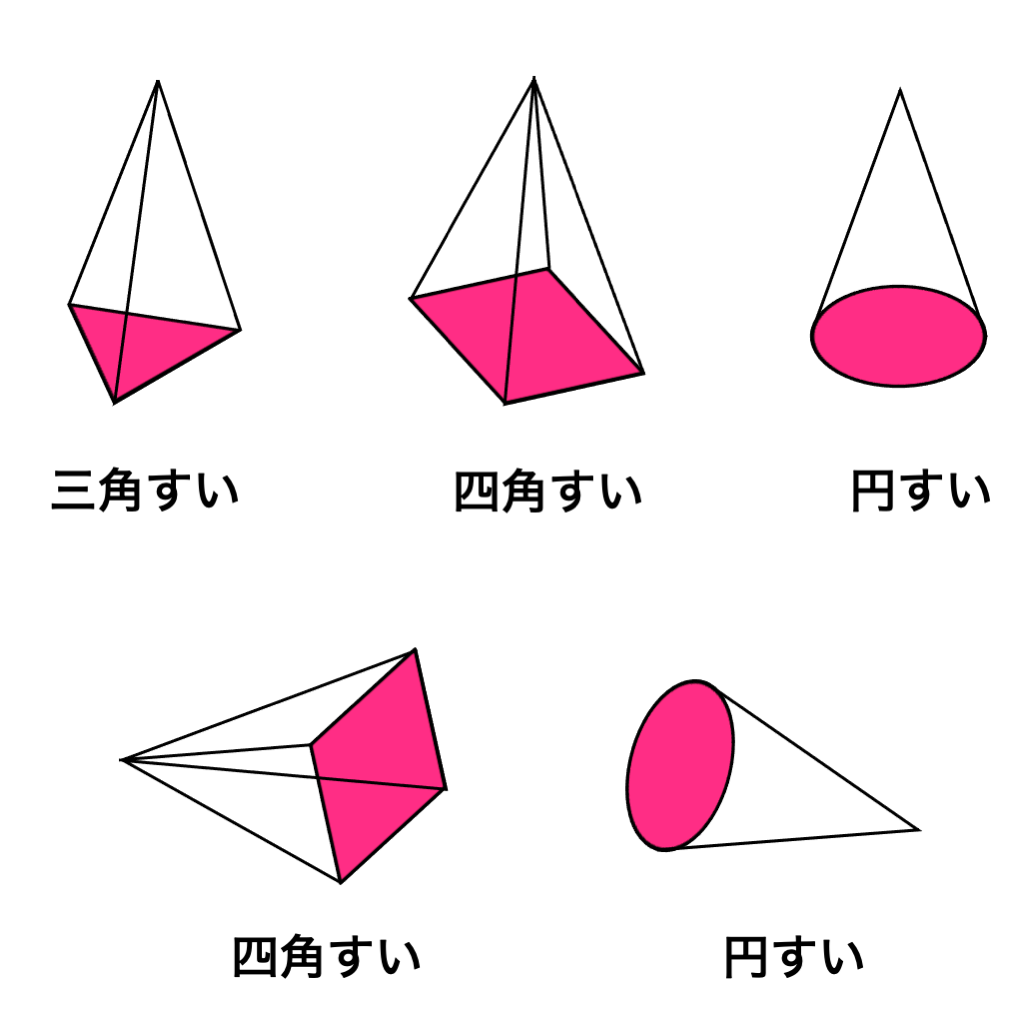

角柱や円柱の先が細くなって一点に集まっている形を錐(すい)っていうんだね。
赤い色の部分が少しずつ小さくなりながら、下から上までずっと同じ形になっているね。


横に倒しても三角すいや円すい おかえりというんだね。
ポイント

図の赤い部分が少しずつ小さくなりながら積み重なって、一点に集まってできた図形を角すいや円すいといいます。
色のついた部分を底面といいます。
底面の形が三角形なら三角すい、四角形なら四角すい、円なら円すいといいます。
横に倒していても、同じ形が積み重なる部分を底面といいます。

上から見るといろいろな形だけど、真横から見ると全部三角形に見えるよ!

ポイント
角すいや円すいは真横(正面)から見ると、三角形に見えます。

体積はどうやって求めればいいのかな。
角柱や円柱みたいに、底面積と高さを使えば求められるのかな。

ポイント
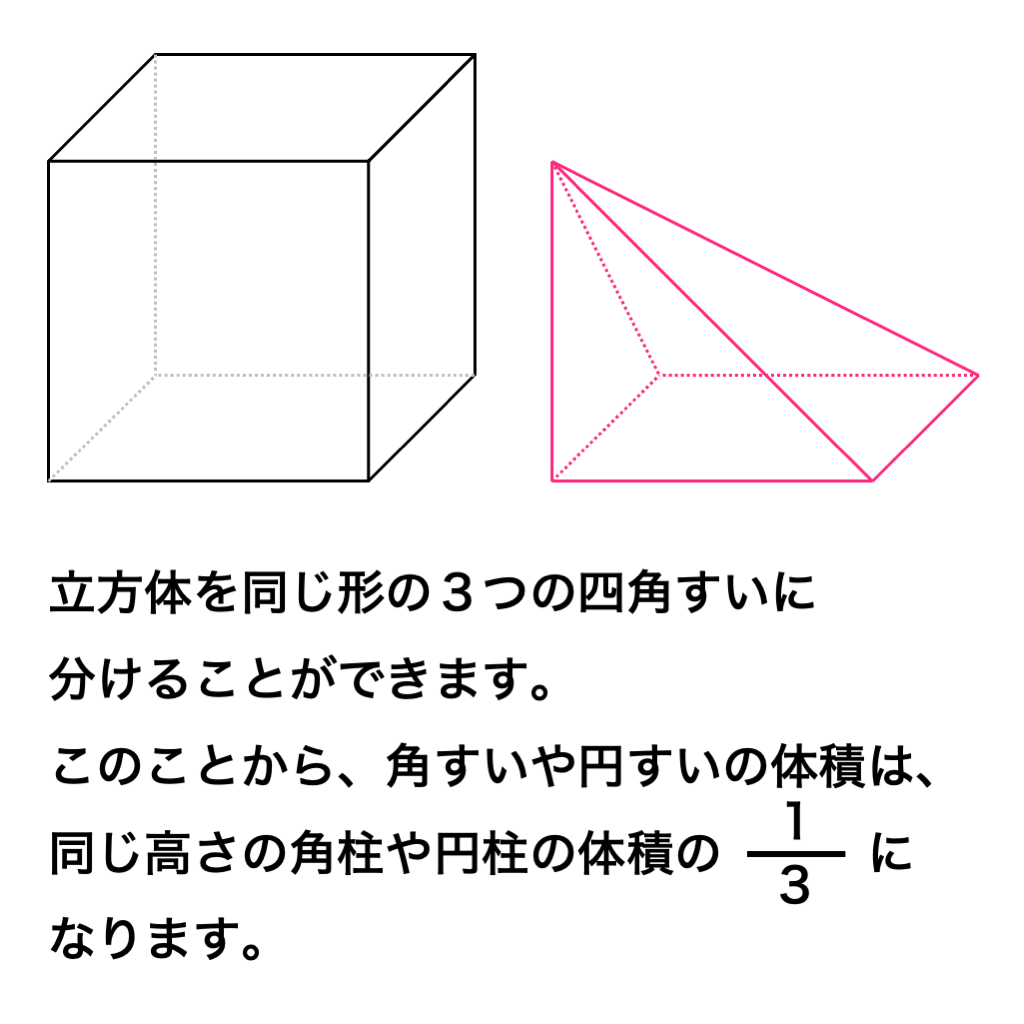
【角すいや円すいの体積=底面積×高さ×3分の1】
問題00318
タブをクリックして答えを確認する
底面の半径が3cm、高さが10cmの円すいの体積を求めましょう。円周率は3.14とします。

球はどうすればいいのかな。
円の面積を求めるときに小さな三角形にして考えたみたいに、小さな円すいが集まっていると考えれば求められるかもしれないよ。

ポイント
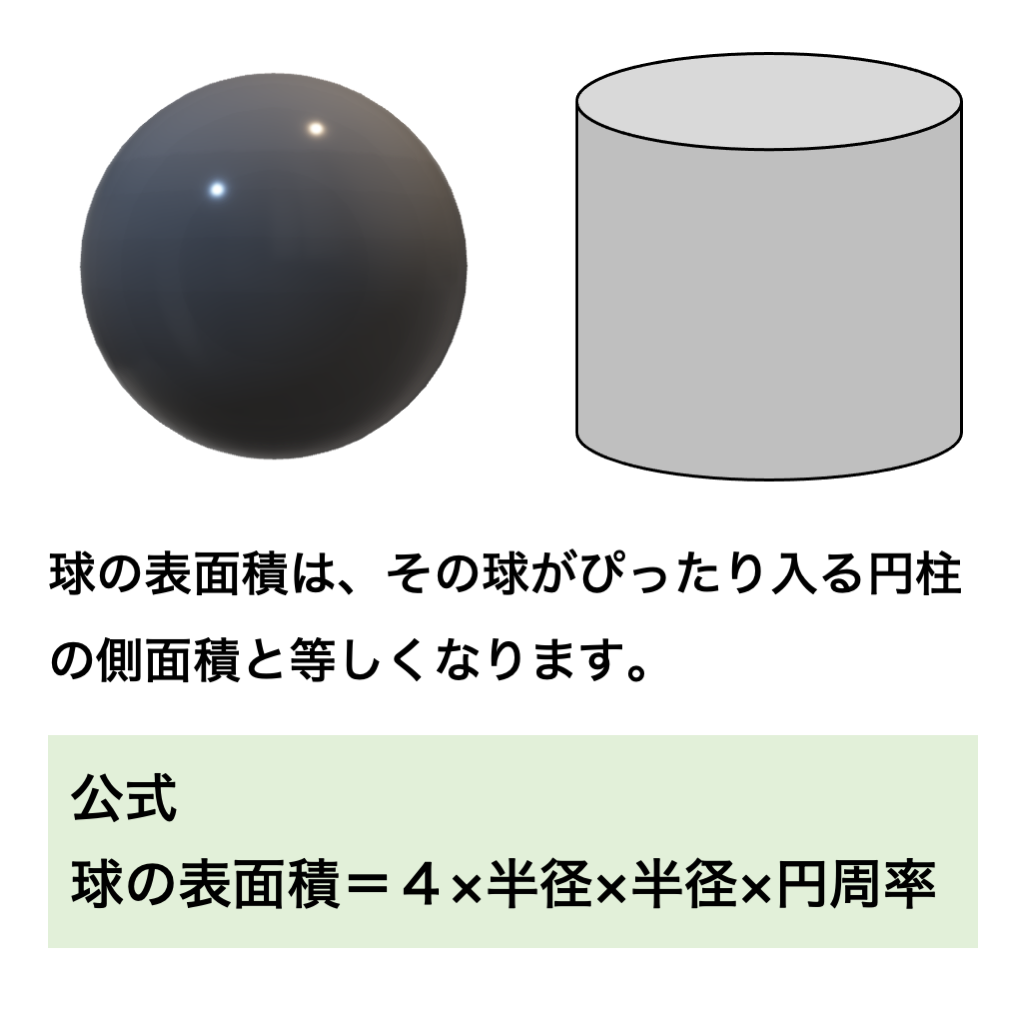

公式を使えば球の表面積を求めることができるんだね。
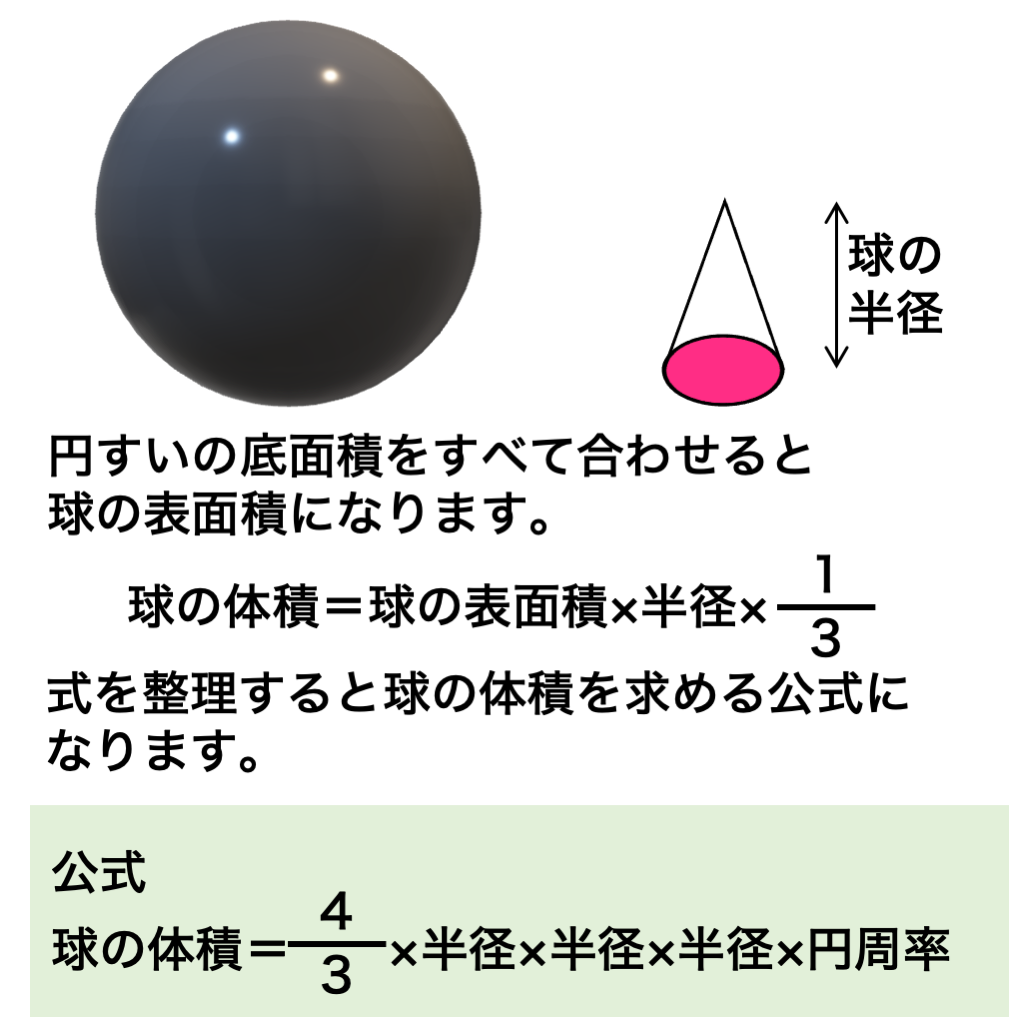
表面積と半径を使えば小さな円すいの体積を求めることができるんじゃない?

ポイント
問題00319
タブをクリックして答えを確認する
半径が3cmの球の表面積と体積を求めましょう。円周率は3.14とします。

半径と円周率を使えば、球の体積を求めることができるんだね。
面積や体積を求める公式がたくさんあるから、しっかり確認しておかないとね。

