台形やひし形やたこ形、その他の四角形の面積の求め方を考えましょう。

平行四辺形や三角形の面積を求めたときと同じように、面積を求められる形に変えるといいのかな?
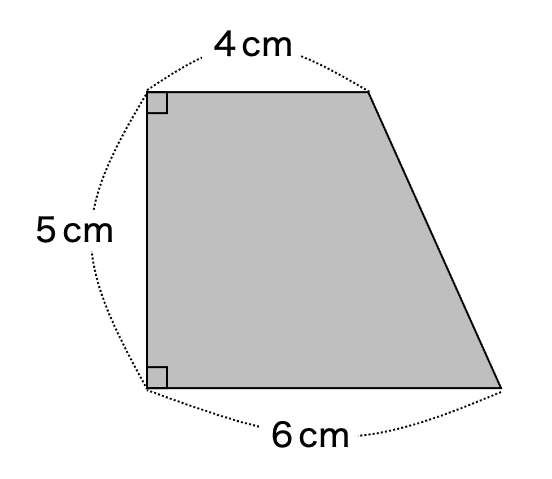
この台形を長方形や平行四辺形、三角形に形を変えれば面積を求められるね。


こうすれば長方形になったよ。
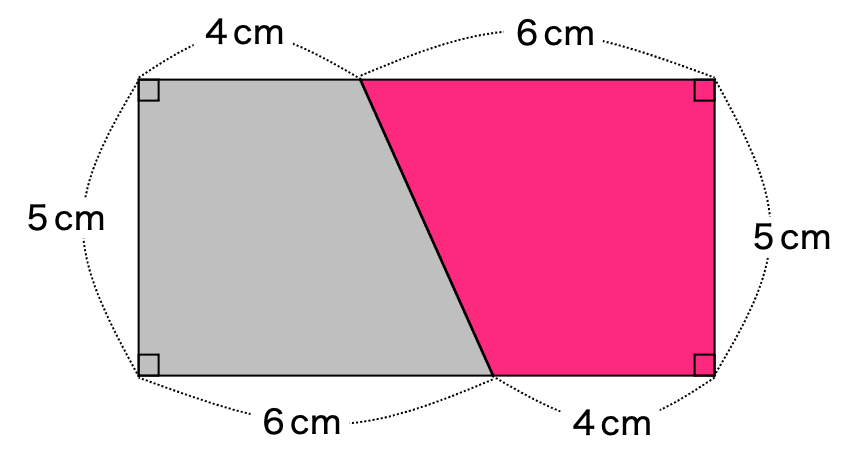
たて5cm よこ6cm+4cm=10cm
長方形の面積 5×10=50
台形の面積は長方形の面積の半分(÷2)なので 50÷2=25
答え 25㎠
こうすれば平行四辺形にもできるよ。

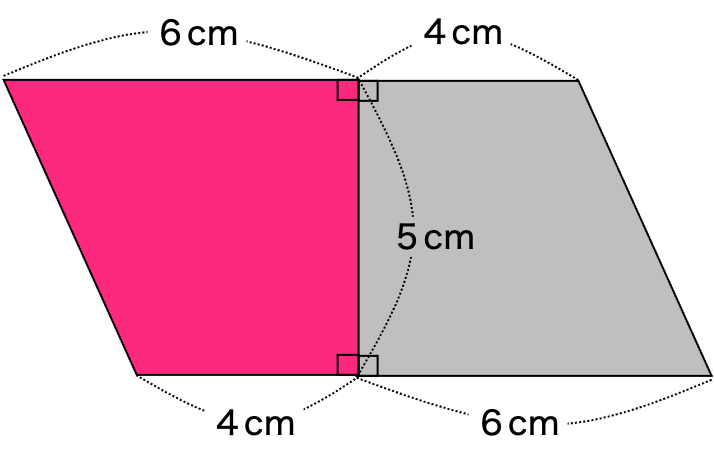
底辺 4cm+6cm=10cm 高さ 5cm
平行四辺形の面積 10×5=50
台形の面積は長方形の面積の半分(÷2)なので 50÷2=25
答え 25㎠

こんなふうに2つの三角形に分けることもできるよ。
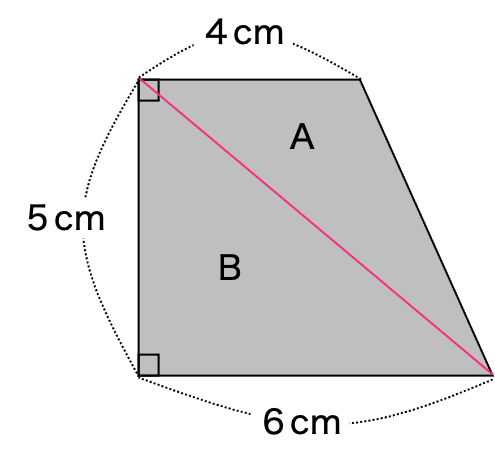
Aの三角形の面積 4×5÷2=10
Bの三角形の面積 6×5÷2=15
AとB合わせると 10+15=25
答え 25㎠
どの考え方でも答えは25㎠になったね。


台形の面積は、平行四辺形や長方形や三角形などに形を変えて求めます。
台形の4cmの部分を「上底(じょうてい)」といい、6cmの部分を「下底(かてい)」といいます。
平行四辺形、長方形、三角形のどの方法であっても、上底と下底と高さを使って面積を求めることができます。
台形の面積を求める公式
台形の面積=(上底+下底)×高さ÷2
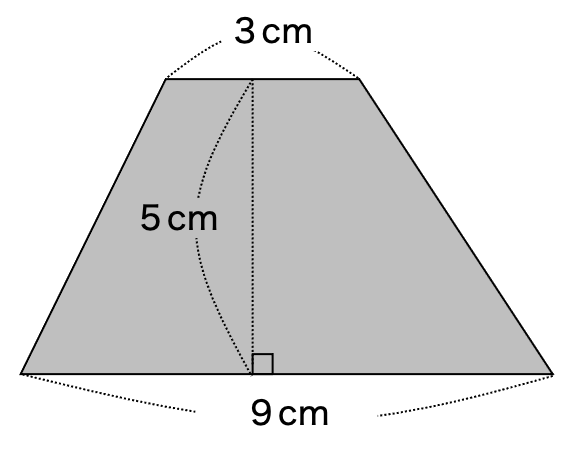
問題00304
次の台形の面積を求めましょう。
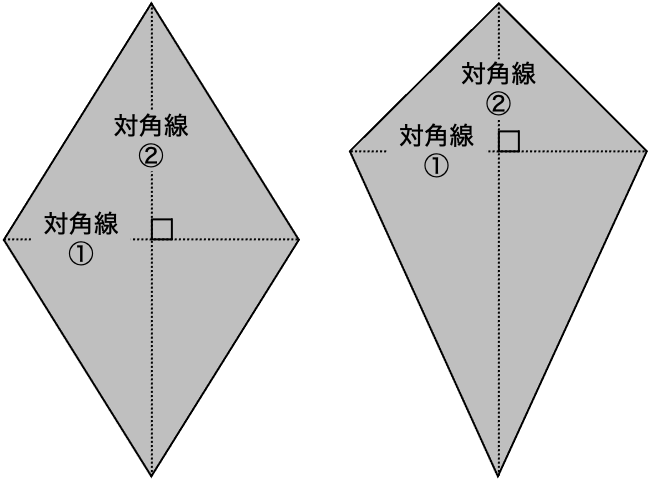
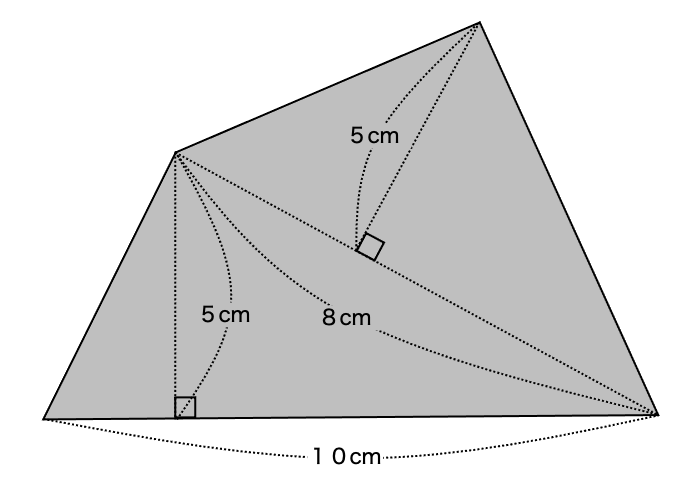
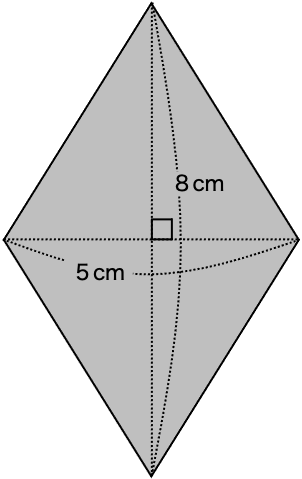
ひし形やたこ形は、対角線が垂直に交わっているのが特ちょうです。
そのため、対角線の長さを使って面積を求めることができます。
ひし形とたこ形の面積を求める公式
ひし形の面積=対角線①×対角線②÷2
たこ形の面積=対角線①×対角線②÷2

え?なんで?
対角線①を底辺とした2つの三角形に分けて考えればいいんだよ。


そうすると、対角線②は三角形の高さになるんだね。
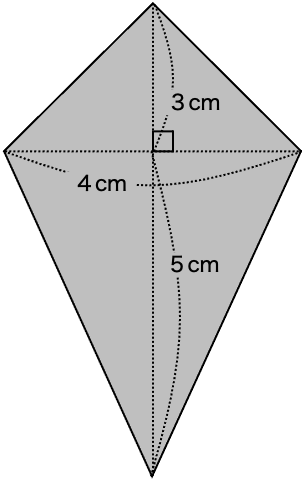
上の三角形の面積 4×3÷2=6
下の三角形の面積 4×5÷2=10
合わせると 6+10=16
対角線を分けたときの長さがわからなくてもだいじょうぶなのかな?


上の図のたこ形の面積を求める式を1つの式にまとめると、
4×3÷2+4×5÷2 となります。
4と÷2がどちらにもあるので、計算のきまりを使って整理すると、
4×(3+5)÷2 というように式を直すことができます。
(3+5)の部分は合わせると対角線②の部分の長さになるので、ひし形とたこ形では、どこで対角線が交わっていたとしても、【対角線①×対角線②÷2】で面積を求めることができます。
問題00305
次のひし形の面積を求めましょう。

それ以外のいろいろな四角形の面積を求めるにはどうすればいいのかな?
四角形は、対角線を1本引くと、全部2つの三角形に分けることができるよ。


三角形に分ければ、底辺と高さがわかれば面積を求めることができるね。
底辺に垂直な直線の長さが高さだから、まちがえないように気をつけよう。

問題00306
次の四角形の面積を求めましょう。