平行四辺形と三角形の面積の求め方を考えましょう。

長方形や正方形の面積の求め方ならわかるよ。
長方形の面積=たて×よこ
正方形の面積=1辺×1辺
だったよね。



長方形や正方形も平行四辺形の仲間だから、同じ求め方でいいのかな?
1㎠の正方形が何個分あるかを数える時に、ななめの部分があると正方形をならべられないね。

平行四辺形の面積は、形の特ちょうに注目して、面積の求め方がわかっている長方形に形を変えれば求めることができます。

どうやって長方形に形を変えればいいのかな?
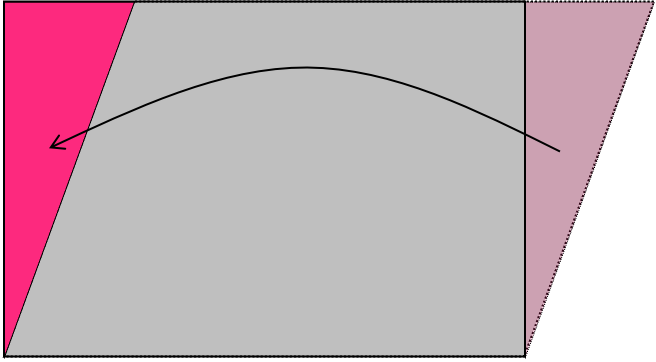
三角形を切り取って動かすのはどう?


真ん中で切って動かすこともできるよ。
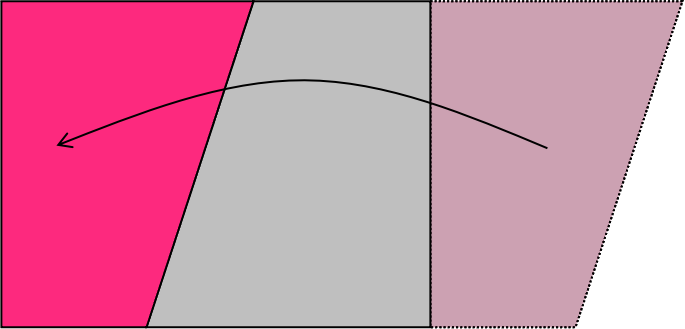
平行四辺形を長方形にできたから、面積を求めることができるね。

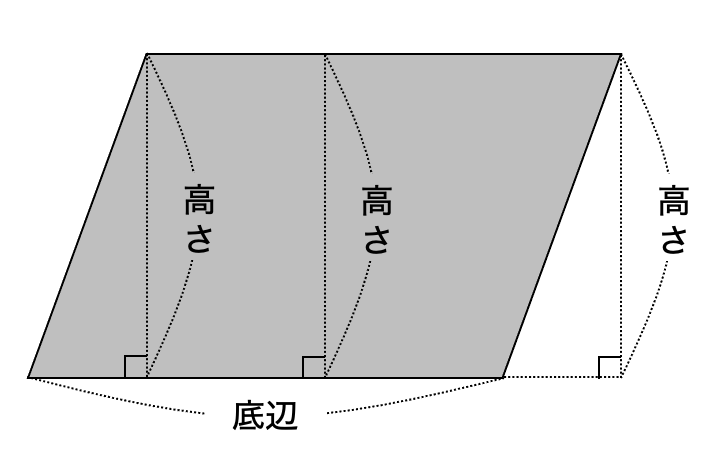
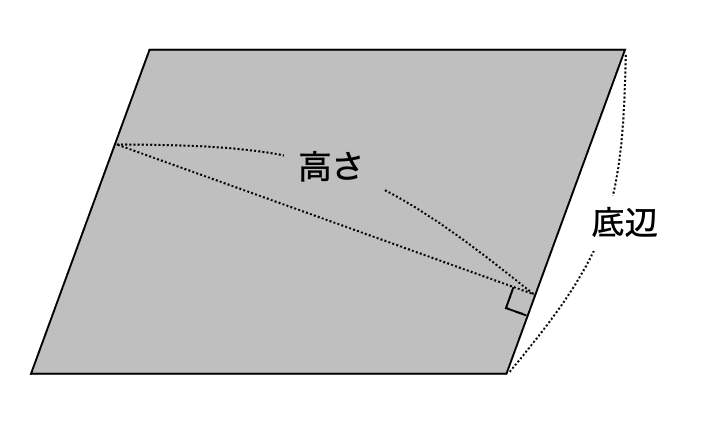
平行四辺形のある1辺を底辺(ていへん)としたとき、その底辺に垂直な直線の長さを高さ(たかさ)といいます。
高さは、平行四辺形の外側でも同じ高さになります。
底辺は図の下側とはかぎらないので、右の図のような底辺と高さになることもあります。
【長方形の面積=たて×よこ】ですので、長方形に形を変えた平行四辺形の底辺は「よこ」と同じ長さ、高さは「たて」と同じ長さになります。
そのため、平行四辺形の面積は、次の公式で求めることができます。
平行四辺形の面積=底辺×高さ
問題00301
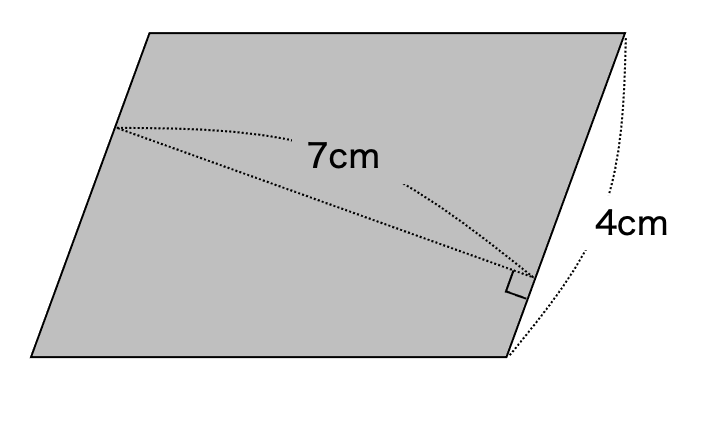
次の平行四辺形の面積を求めましょう。
①

②

三角形はどのように面積を求めればいいのかな?

長方形や平行四辺形に形を変えれば求められそうだね。


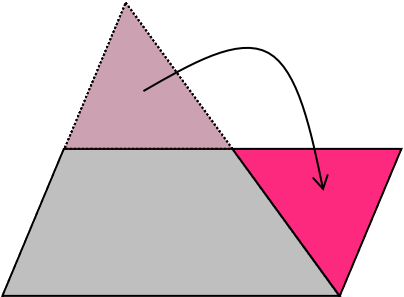
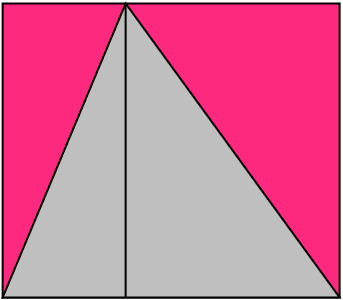

左の図は、ひっくり返して2こならべたら平行四辺形になったよ。
真ん中の図は、高さのちょうど半分のところで切って動かしたら平行四辺形になったよ。


右の図は、三角形を切って2つ合わせたら、長方形になったよ。
平行四辺形や長方形にすることはできたけど、三角形が2こになったり、高さが半分になったりしちゃうね。

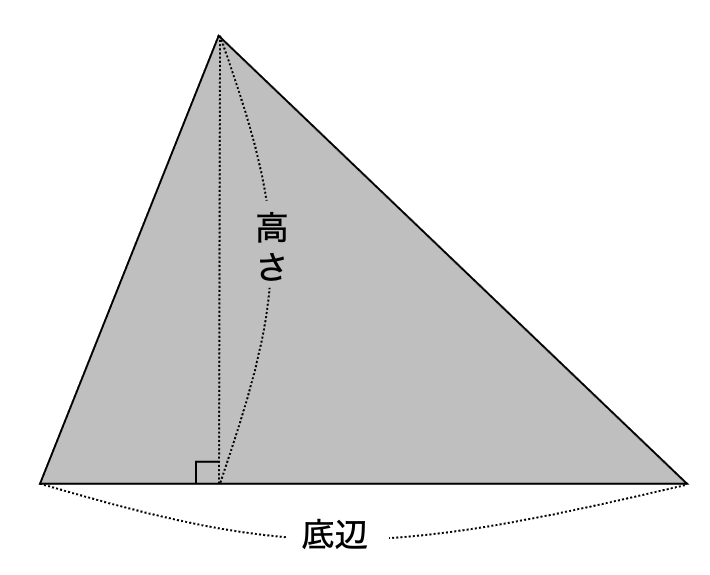
三角形のある1辺を底辺(ていへん)としたとき、その底辺に垂直な直線の長さを高さ(たかさ)といいます。
高さは、三角形の外側でも同じ高さになります。
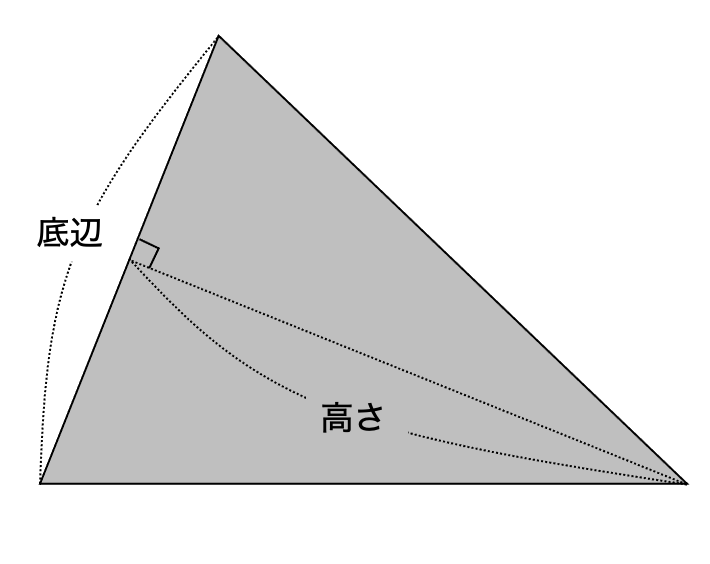
底辺は図の下側とはかぎらないので、右の図のような底辺と高さになることもあります。
三角形を2つ合わせて平行四辺形や長方形にした場合、三角形の面積を求めるには、最後に「÷2」をする必要があります。
高さを半分にして平行四辺形にした場合、高さを「÷2」する必要があります。
【平行四辺形の面積=底辺×高さ】ですので、三角形の面積は、次の公式で求めることができます。
三角形の面積=底辺×高さ÷2
問題00302
次の三角形の面積を求めましょう。
①
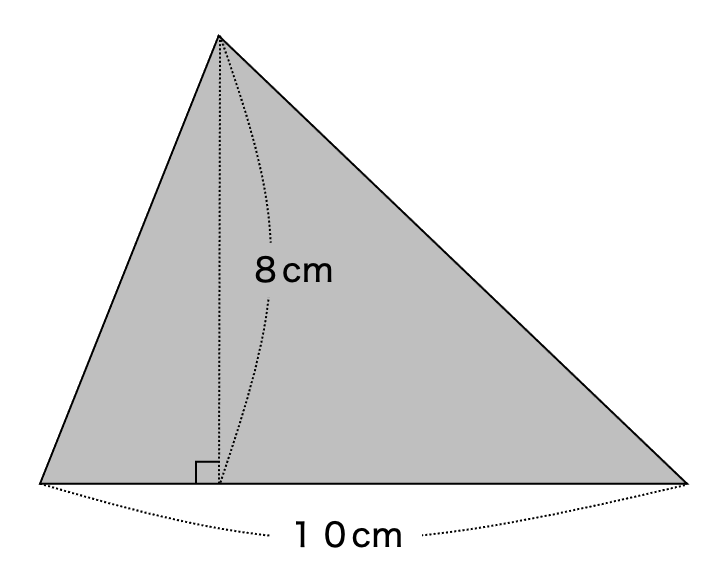
②
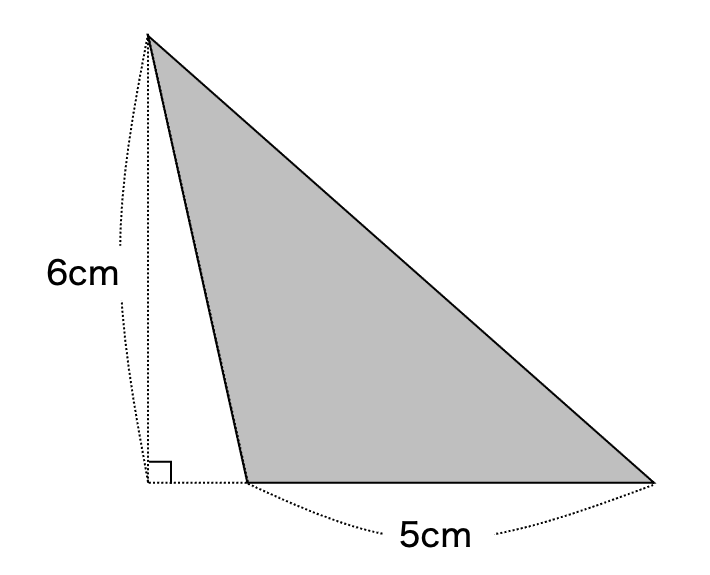

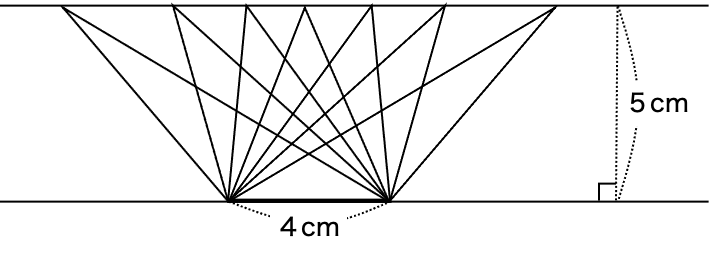
【三角形の面積=底辺×高さ÷2】ということは、次の3つの三角形は、形がちがうけど面積が全部同じだね。
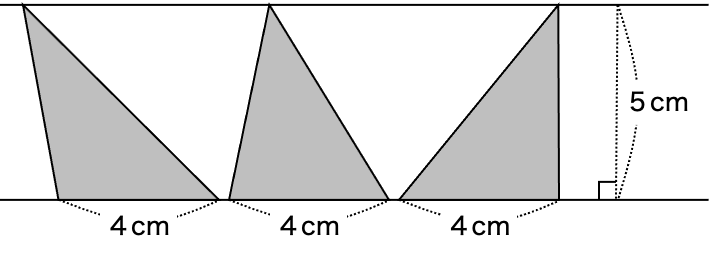
4×5÷2=10
どれも10㎠だね。

底辺と高さが同じであれば、面積を変えずに三角形や平行四辺形の形を変えることができます。
これを等積変形(とうせきへんけい)といいます。