円の面積を計算で求められるようになりましょう。

円周の長さは【直径×円周率】で求められたよね。
円の面積を求めるときにも円周率を使うのかな?

円の面積は、次の公式で求められます。
円の面積=半径×半径×円周率
円周率はπ(ぱい)という記号で表されることがあります。

半径の長さと円周率を使えば、円の面積を計算で求められるんだね。
でもなんで?

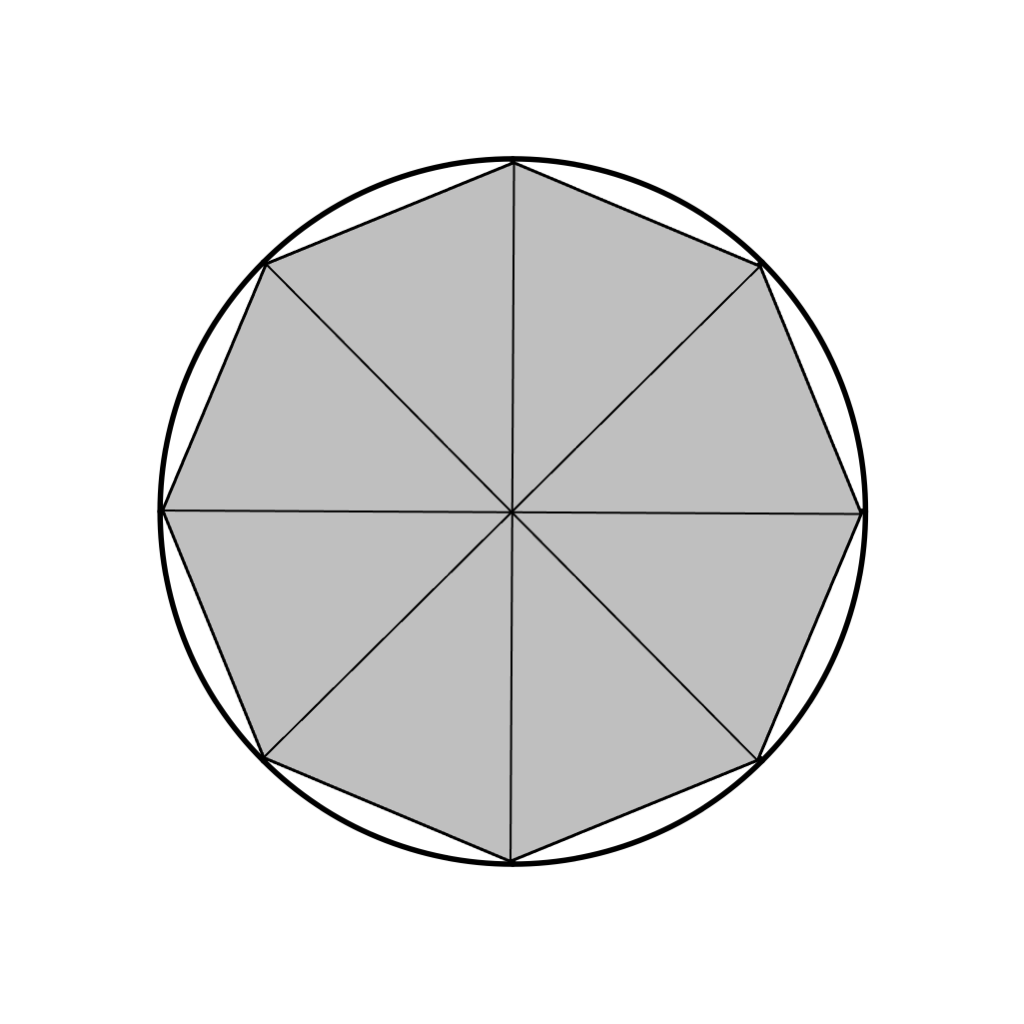

円の中に正多角形をかいていきます。正八角形よりも、正十二角形の方が、円の形に近づいています。
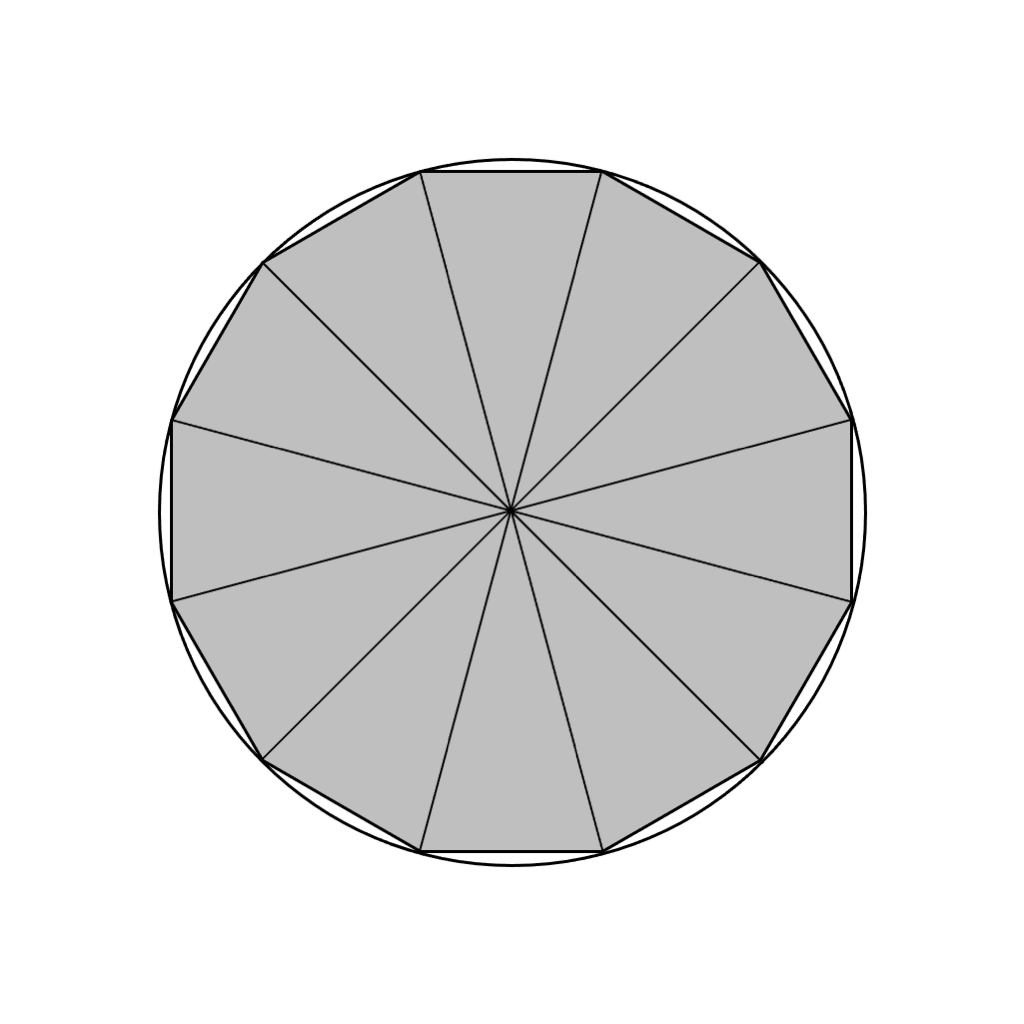
右の図は正三百六十角形をかいたものです。ほぼ円になりました。
正多角形は、半径を二等辺とした三角形に分けることができます。
三角形にすれば、【三角形の面積=底辺×高さ÷2】で面積を求めることができます。
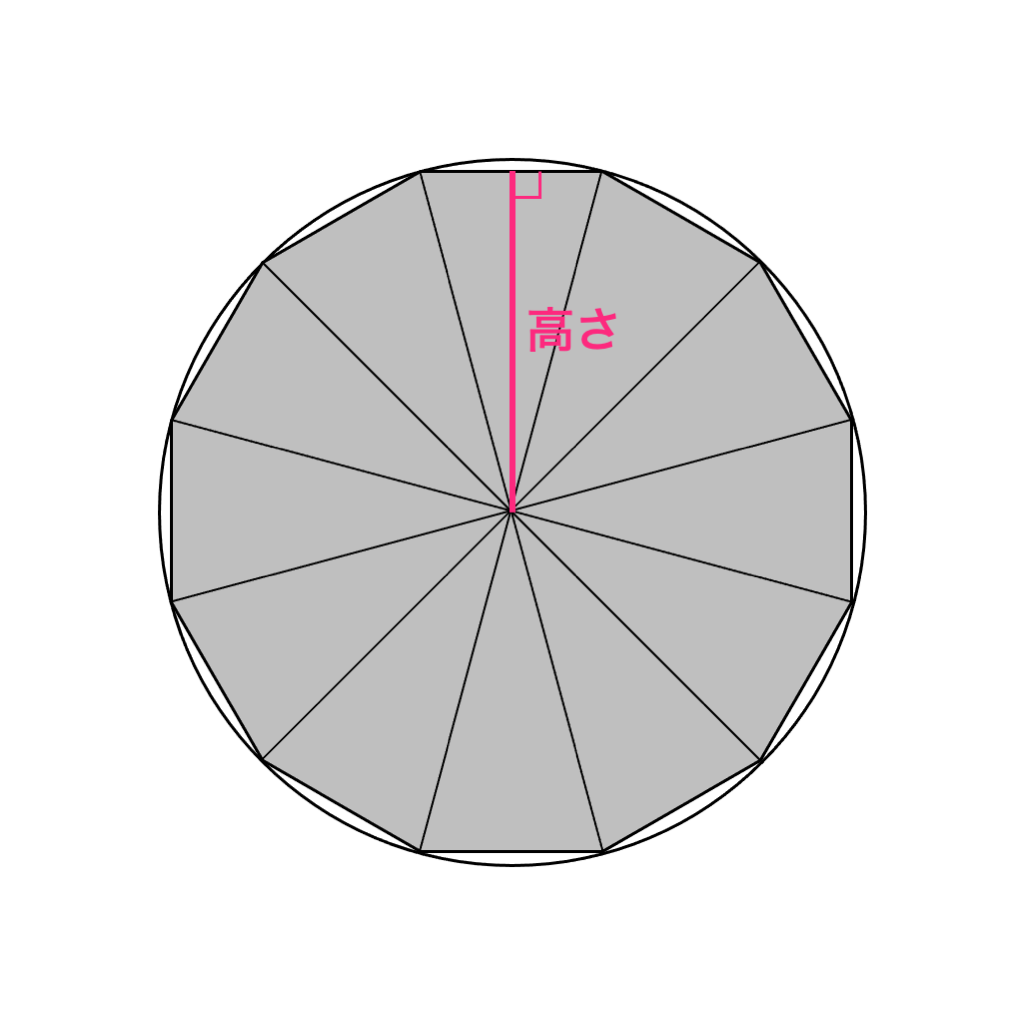
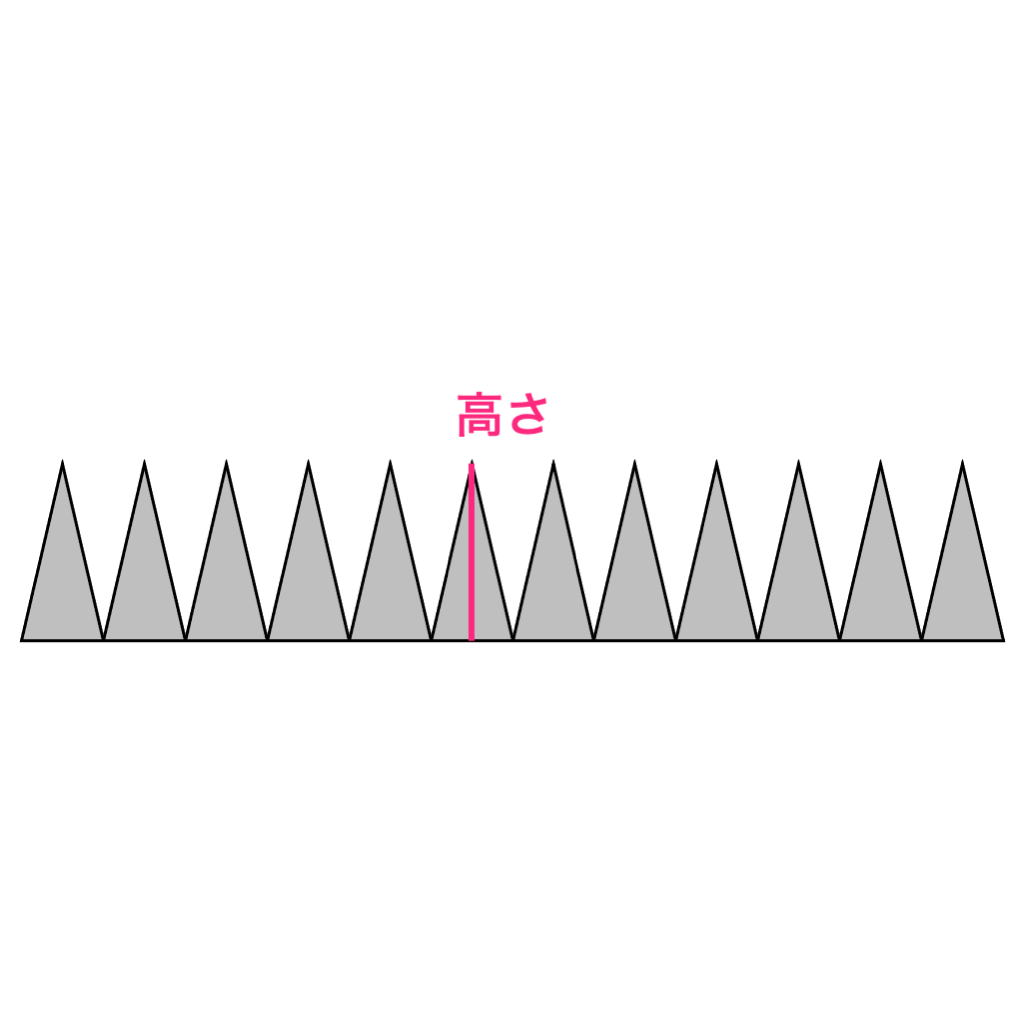
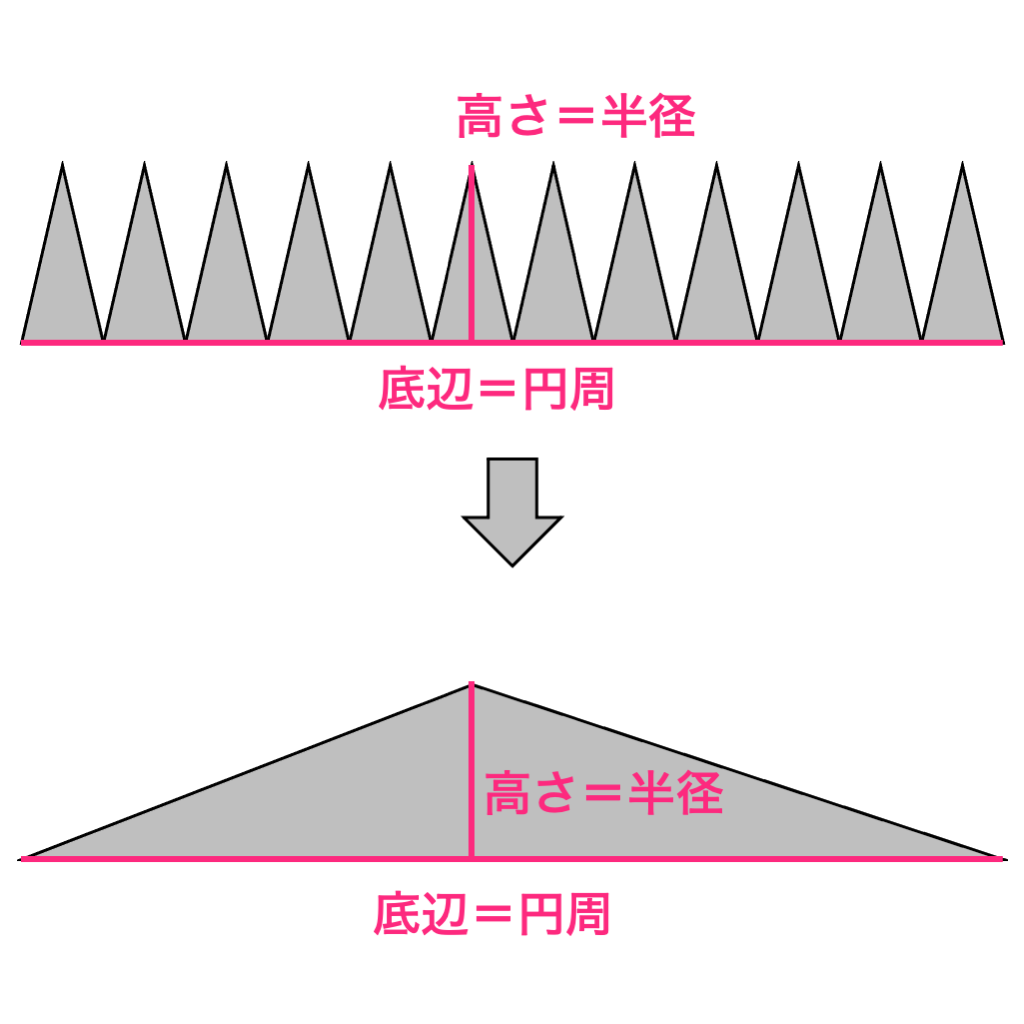
正三百六十角形くらいになると、底辺は円周、高さは半径とほぼ同じになります。
もっと細かく細かく三角形に分ければ、底辺は円周、高さは半径と同じになります。
【円周=直径×円周率】ですから、
【円の面積=(直径×円周率)×半径÷2】となります。
【直径÷2=半径】なので、上の式を整理すると
【円の面積=半径×半径×円周率】となります。

小さな三角形に分けていくっていうのはすごいアイデアだね!!
高さが同じ三角形の等積変形を使うっていうのもよく考えているね。

問題00314
① 半径が4cmの円の面積を求めましょう。円周率は3.14とします。
② 直径が6cmの円の面積を求めましょう。円周率は3.14とします。
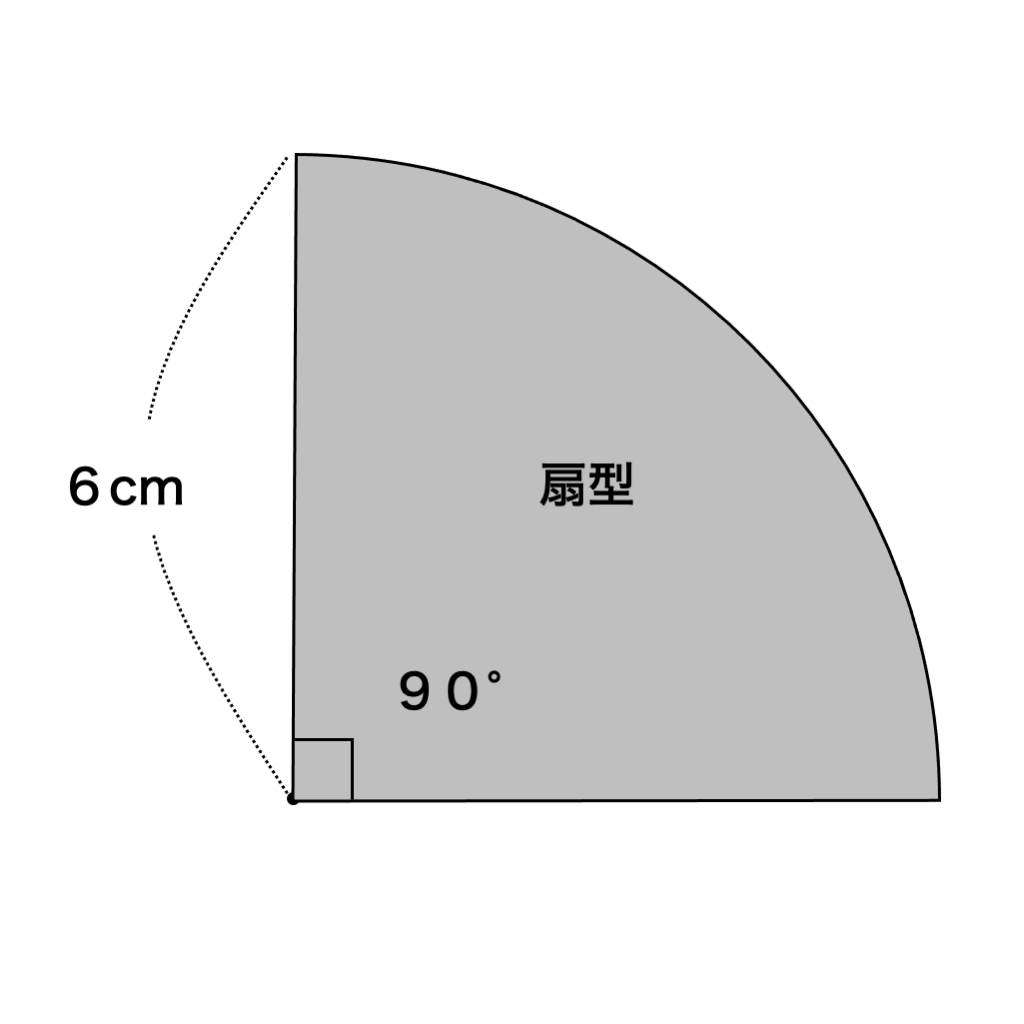
扇型の面積は、中心角の大きさによって比例します。
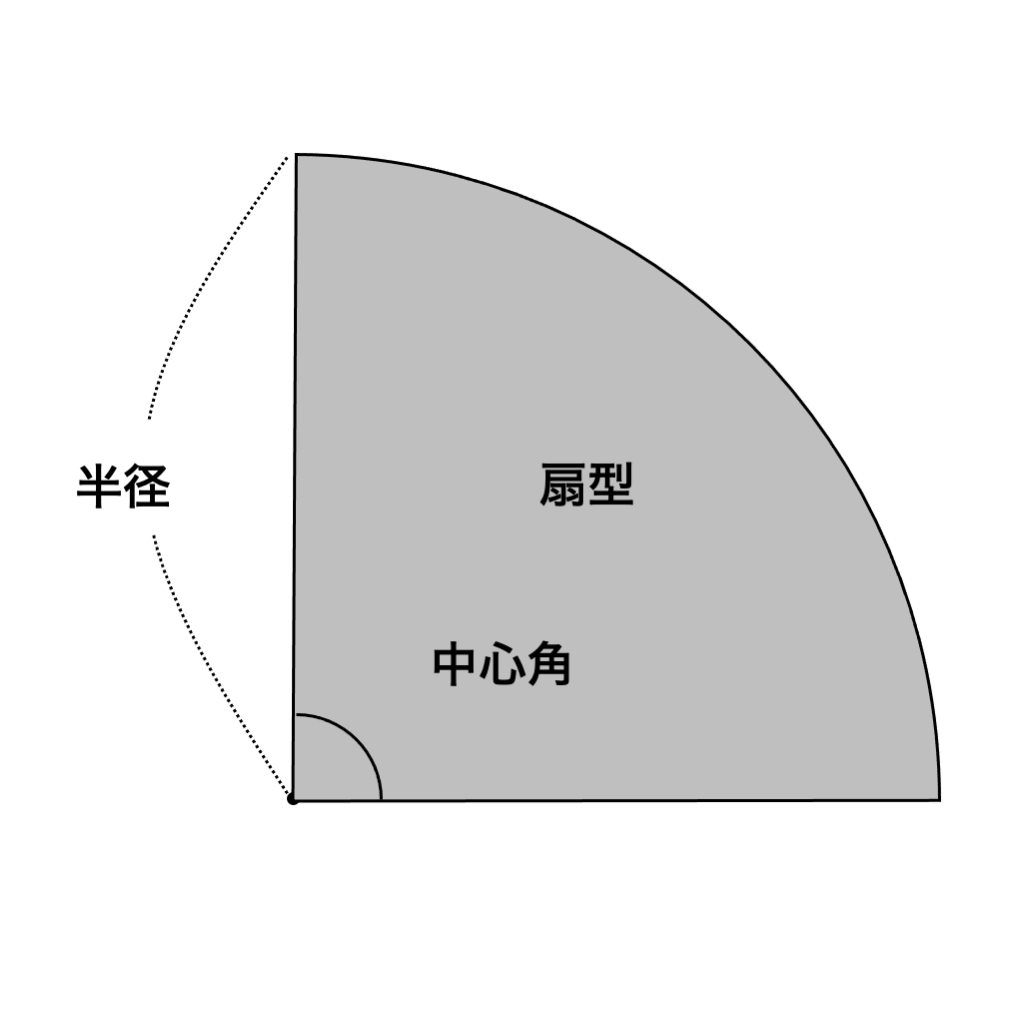
円の中心の角度は360°なので、例えば中心角が90°の場合、4等分したうちの1つ分ということになるので
【中心角が90°の扇型の面積=半径×半径×円周率÷4】
という式で求めることができます。
中心角が180°の半円の場合は、
【半円の扇型の面積=半径×半径×円周率÷2】
という式で求めることができます。
円を等分することができない場合には
【扇型の面積=半径×半径×円周率×中心角÷360】
という式で求めることができます。

扇型の円弧の長さを求めるときと同じような考え方だね。
計算が大変だぁ・・・

問題00315
半径が6cm、中心角が90°の扇型の面積を求めましょう。円周率は3.14とします。